Maple入門
Maple (メイプル)
とは,数式処理,数値計算,グラフ作成などを行うソフトウェアです.Mapleは,カナダのウォータールー大学で開発され,日本ではサイバネットシステム
社が販売,翻訳を行っている.Mapleを使うと,紙と鉛筆で行う数学の計算や作図をコンピュータで行うことができます.
今回はMapleの基本的な使い方を説明します
興味のある人はインターネットに関連するWebがたくさんあるので検索してみましょう.
Mapleを使ってみる
Mapleの起動
1.デスクトップ下のドッグの中の”Finder”をクリック
2.Finderの左側の”アプリケーション”をクリック
3.フォルダ”Maple10”をダブルクリック
4.フォルダMaple10の中のMaple10をダブルクリック
という手続きで起動できます.
*良く使用するソフトは,デスクトップ下のドッグの中にショートカットを
作っておくと便利です.
作り方は,単に,Maple10を左クリックでドラッグしてドックに入れれば良いです.
同じ操作を,ターミナルやFireFoxなど良く使うソフトで行っておくと,
PCが使いやすくなります.
自分専用のデスクトップを作りましょう.
*キーボード下の”Fn”キーと”9(数字)”キーを同時に押すと,画面上に表示されているウインドウすべてが,小さく表示されて選択しやすくなります.
たくさんウインドウを開いているときには便利です.
Mapleの基本操作
以下,読みながら自分でMapleを動かしてみてください.
まず.次のように打ち込んでみてください.
1+2;
「1+2;」を入力したあと[Enter]キーを押します.; は数式の終わりを意味する
区切りの文字です(なくても動きますが入れるのが正式のようです).
するとMapleは計算を実行して,答えの3を表示します..
3 (1)
今度は,
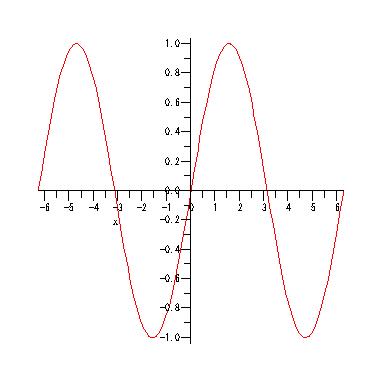
plot(sin(x), x = -2*Pi .. 2*Pi);
と入力してみてください.(円周率πは,Mapleでは,Piと表記します.Pは大文字)
すると下のように,グラフが表示されます.
Mapleには詳しいヘルプファイルが付いています.ヘルプを呼び出すのも
計算と同じところに,
?plot;
と入力するだけです.しばらく(20秒くらい)するとヘルプが出てきます.
コマンドの使い方が分からないときは,ヘルプを参照してください.
画面左のメニュー
キーボードからの入力の代わりに,画面左のメニューから入力内容を選ぶこともできます.
例えば,[数式]をクリックすると,三角関数,微積分など,
良く使用する数式のテンプレートが現われます.
それらをクリックすることで数式を入力することができます.
関数の二次元プロットの作成
plot(関数, 水平方向の範囲, 垂直方向の範囲)
は,関数の二次元グラフを表示(プロット)させるための命令です.
範囲の入力は,x=0..10のように書きます.
これで,0 ≤ x ≤ 10の範囲を表示させることができます.
垂直方向の範囲は省略でます.
plot( [関数1,関数2,関数3], 水平方向の範囲, 垂直方向の範囲)
で複数の関数をプロットすることができます.次のように入力してみてください.
plot( [x, x^2, x^3, x^4], x=-10..10, y=-10..10);
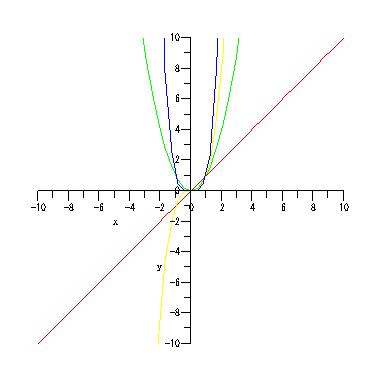
関数の定義
次のように入力すると関数を定義できます.
f := x -> 7*sin(x) + sin(7*x);
これで,関数 fを f(x)=7*sin(x) + sin(7*x) と定義できました.
f := x -> (xを変数とする関数の式)
とすることで,関数 f(x) を定義できるわけです.
この状態で,
plot( f(x), x=0..10);
とすれば,関数のグラフが得られます.
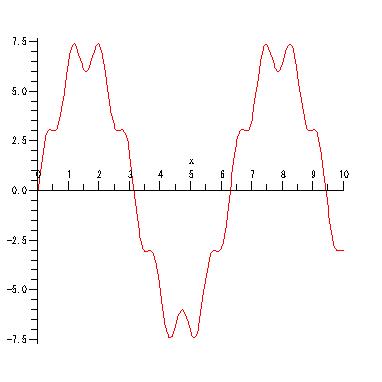
また,
f(a);
とすることで,f(x)のxにaを代入した式.つまりf(a)を展開した式を得ることもできます.
また,
b:=Pi/2
f(b);
のように,定数を定義することもできます.
以降,bは数値(π/2)として扱われます.
定義を初期化するときは,
restart;
とします.
関数を区分ごとの定義
f := x -> piecewise(x < 0, cos(x), x>=0, 1+x^2);
plot( f(x), x=-5..5);
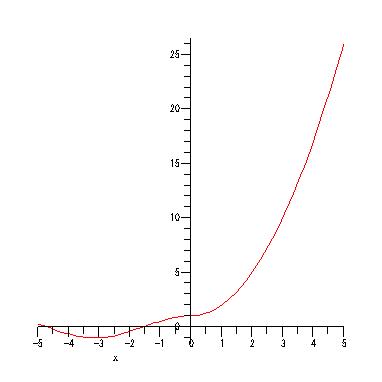
piecewise は関数を区分ごとに定義するための仕組みです.
piecewise(xの範囲1, 関数1, xの範囲2, 関数2, ....,その他のxの範囲の場合の関数)
という使い方をします.
不連続点を持つ関数
f := x -> piecewise(x<1, -1, x<2, 1, 3)
plot(f(x), x=0..3);
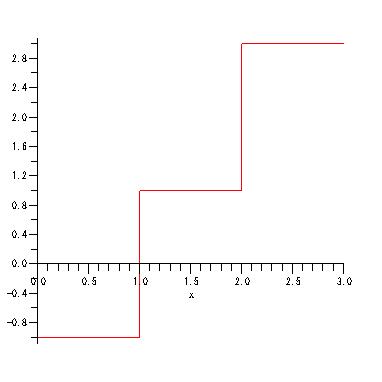
plot(f(x), x=0..3, discont=true);
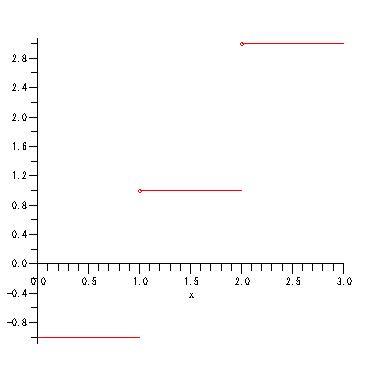
discont=trueでグラフ描画時に不連続点を直線でつながないようにできます.
媒介変数を用いた表現
plot( [ cos(t), sin(t), t=0..2*Pi ], scaling=constrained);
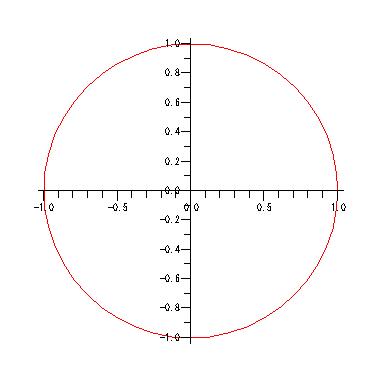
plot( [ x(t), y(t), tの範囲 ] )
という使い方で,陰関数も表示できます.
scaling=constrained
は横軸と縦軸の寸法比を同じにする命令です.
scaling=unconstrained
とすれば,自動で適切なサイズ比になります.
極座標を用いた表現
with(plots);
polarplot(1, theta=0..2*Pi, scaling=constrained);
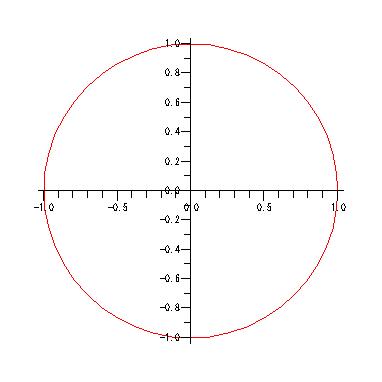
polarplot( rの条件式, θの条件式 )
とすることで,極座標系に関数をプロットできます.
普通のプロットと同様に,媒介変数を用いることもできます.
polarplot( [ sin(t), cos(t), t=0..2*Pi ] );
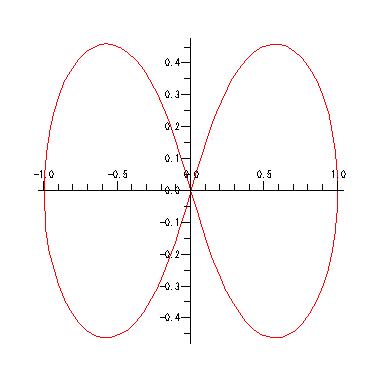
polarplot( [ r(t), θ(t), tの範囲 ] ) という形式です.
微分,偏微分
偏微分は
diff(f(x) , x);
微分は
D(f)(x);
です.
?diff;
?D;
で詳細をみてください.
f := x -> x^3;
plot([f(x),diff(f(x),x),diff(f(x),x,x)],x=-10..10);
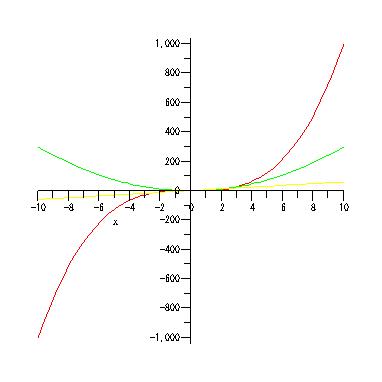
アニメーション
Mapledでは,以下のようなグラフのアニメーションを簡単に作成できます.
アニメーションを行うにはまずグラフ描画パッケージ plots を利用することを
システムに伝える必要があります.
with(plots);
次にアニメーションつきのグラフを描画させます.
animate( sin(x*t), x=-10..10, t=1..2, frames=50 );
最後のframes=Xは,アニメーションのコマ数を指定しています.
グラフははじめはアニメーションしていません.
グラフをクリックするとMapleのウィンドウの上部に現われる黄色い再生ボタンを押すと,
アニメーションがはじまります.
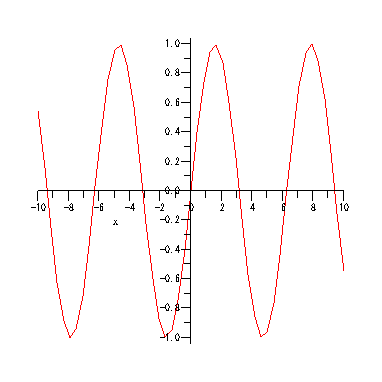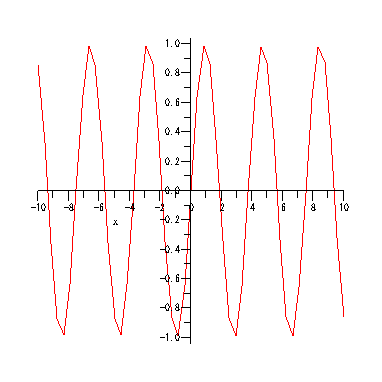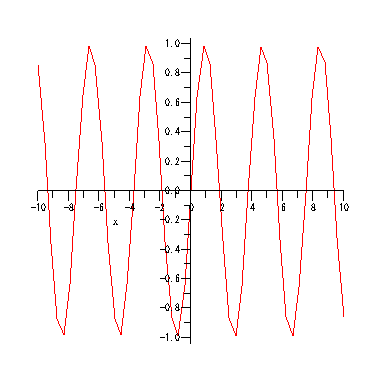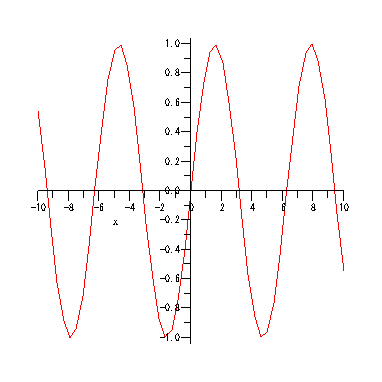
animate( plot3d, [y*sin(x*t), x=-5..5, y=-5..5], t=1..2)
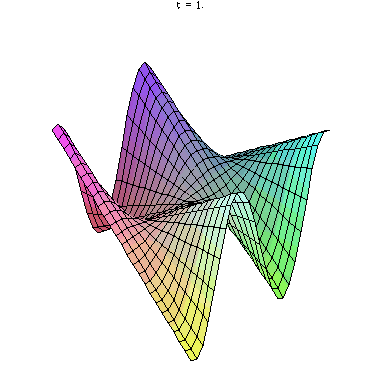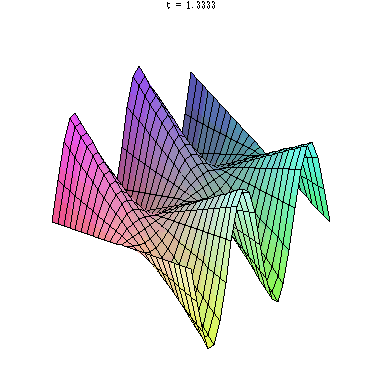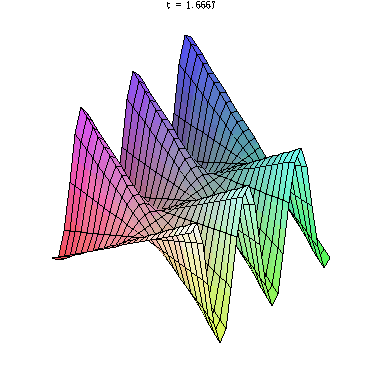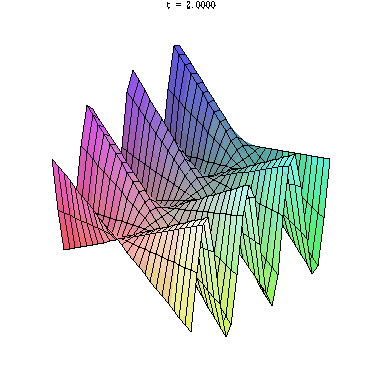
?animate でヘルプを見ておきましょう.
グラフの操作
作成した画像や動画は,右クリックすると,様々なメニューが表示されます.
"スタイル","色","照明","軸","スケールの変更"
"光沢度","透明度","操作","アニメーション"
これらはグラフの表示形式をカスタマイズできます.
見やすい形式や視点を探してみてください.
"エクスポート"により,作成した画像,動画を保存できます.
Tex用の画像にしたいならば,"EPS形式"で保存すればよいでしょう.
動画(gifアニメーション)として保存し,Webページに動画を掲載するには,"GIF形式"で保存します.
画像の形式を示す拡張子(.eps, .gif, .jpgなど)は,
画像をエクスポートした際に自動的に名前の後ろに付きます.
その他の機能
今回の課題を行うためには必要ありませんが,サイバネットシステム社のページにある
ビギナーズガイドにより詳しい説明があります.
Mapleを使いこなせると,
物理や制御などの問題の見当をつけるのに便利かもしれません.
課題
Webページ作成課題の際に作成したフォルダ(public_html)の中にmaple.htmlを作成して,
maple.htmlの中にアニメーションを掲載し(<IMG src="xxxx.gif">でできます.),
そのグラフの数学的意味または物理的意味を説明をしなさい.
また,グラフを描画するためのコマンドも掲載しなさい.
例:
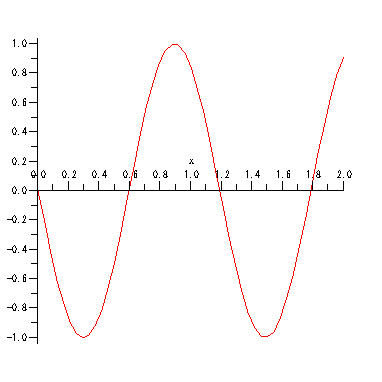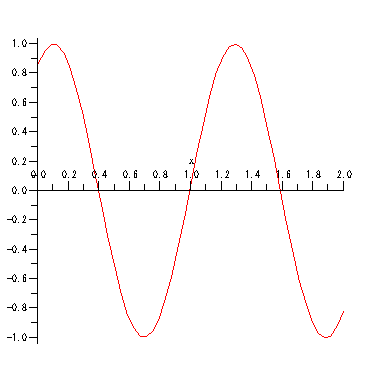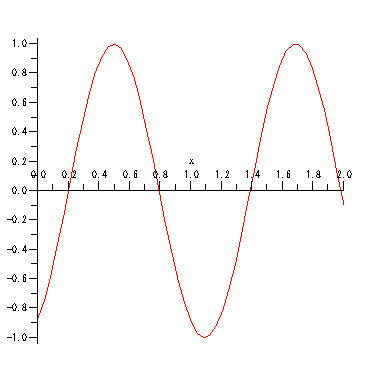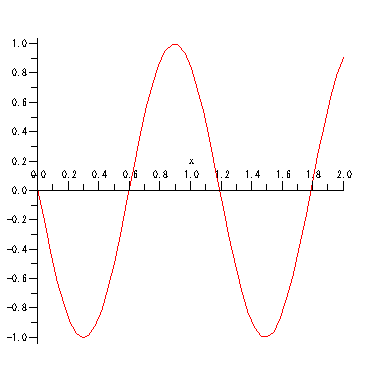
説明:
周期 T=1,振幅 A=1, 波の速度 v=1 の横波.
原点からx+向きに無限に長い糸を用意し,
糸の端を周期T秒,小さな振幅Aで振動させたときに糸に発生する波が(減衰を無視すれば)これに当たる.
波の速度は,糸の密度と張力などで決まる定数.
コマンド:
with(plots);
T := 1;
A := 1;
v := 1;
animate( sin(x + 2*Pi*((t-(x/v)) /T)), x=0..2, t=0..10, frames=100 );
余裕があれば,様々なグラフを作成してそれらの意味を説明しなさい.
課題提出確認: